Cryptographic failures in the wild #
Many developers see security people as annoying creatures, always pointing out mistakes and criticizing incorrect decisions. A cryptographer is considered more malignant: they know math and can tell you actual probabilities of some of your failures. They also yell crypto is not a cryptocurrency and don’t roll your own crypto often. That would be us.
The precise definition of the second proverbial phrase depends on the context and has changed over the last couple of decades, but most of the time it means Do not design your cryptosystems, especially if you don’t know anything about them.
The reasons lie in the security and complexity of the cryptographic systems. But since you hear this phrase over and over, this means many developers still ignore it, and we still continue to find cryptographic failures when reviewing cryptographic systems.

We are here to talk about the consequences of home-brewing faulty cryptosystems using one example, found in the wild, with a critical amount of cryptographic failures per kilobyte of the cryptographic code. Unfortunately, this is also a very piece of code running in numerous devices. Hundreds of thousands, if not millions. The nature of the device has been heavily redacted to protect the guilty.
With cryptographic bugs, it’s often hard to cross the mental bridge between “it is theoretically broken” to “it can be easily exploited”. We hope this post and its modestly entertaining examples could be a usable illustration.
Scroll to the Real-world repercussions section if you are not in the mood of reading.
- Cryptographic protection for radio systems
- Predictable IV in CBC mode
- Exploiting AES-CBC Padding Oracle attack
- Breaking AES-CTR with fixed nonce
- Non-existing integrity protection for CBC and CTR
- Replay attacks
- Encryption key is set to default if invalid is provided
- Real-world repercussions
- Summary
Cryptographic protection for radio systems #
Imagine a remote control toy car. The controller communicates with it and allows the user to accelerate, take turns or stop the car. The whole communication between the controller and the toy car is encrypted.
Roughly speaking, the user moves the joystick on the remote controller, this push is translated into a digital signal via ADC, then passed to the radio modem, which encrypts the digital signal, turns it into radio signal, and sends it. The car receives the signal, decrypts it, performs an action (moves forward, for example), and sends the confirmation back.
This RF cryptosystem has the following threat model:
- This is interactive one-to-one communication. One remote controller is connected to one toy car.
- As communication is based on radio, the adversary can eavesdrop on the traffic (passive MitM), predicting the position and direction of the car.
- An adversary can perform an active MitM by using a powerful radio module “louder” than our radio modem, intercepting the original radio signal, and sending malicious signals to the car while pretending to be its controller.
This remote car is very popular. It’s rather cheap and has an open-source firmware with over 200 forks on GitHub. The firmware is recommended by the official car manufacturer and often used by the community to build advanced and customized toy cars.
Recently, we had to research this “car-controller” system in real life, analyzing its hardware, firmware, and the communication protocol. Despite the popularity and open-source nature of the system, we found numerous flaws in the cryptographic implementation that allows locating, tracking, and even stealing other people’s toy cars!
Predictable IV in CBC mode #
Let’s start with something easy: how the encryption and transmission are performed.
To transmit a data, the protocol divides it into very small packets (say 48 bytes). Each packet is encrypted, then its length and checksum are appended. The encryption can be performed by a hardware-accelerated AES in one of two modes: CBC and CTR.
The CBC, or Cipher Block Chaining, is the way of extending a constant-length cipher into a variable-length one. It works by the following method: the plaintext is divided into blocks. Each block is XORed with a previous ciphertext and the result is encrypted. The first block is XORed with an Initialization Vector or IV.
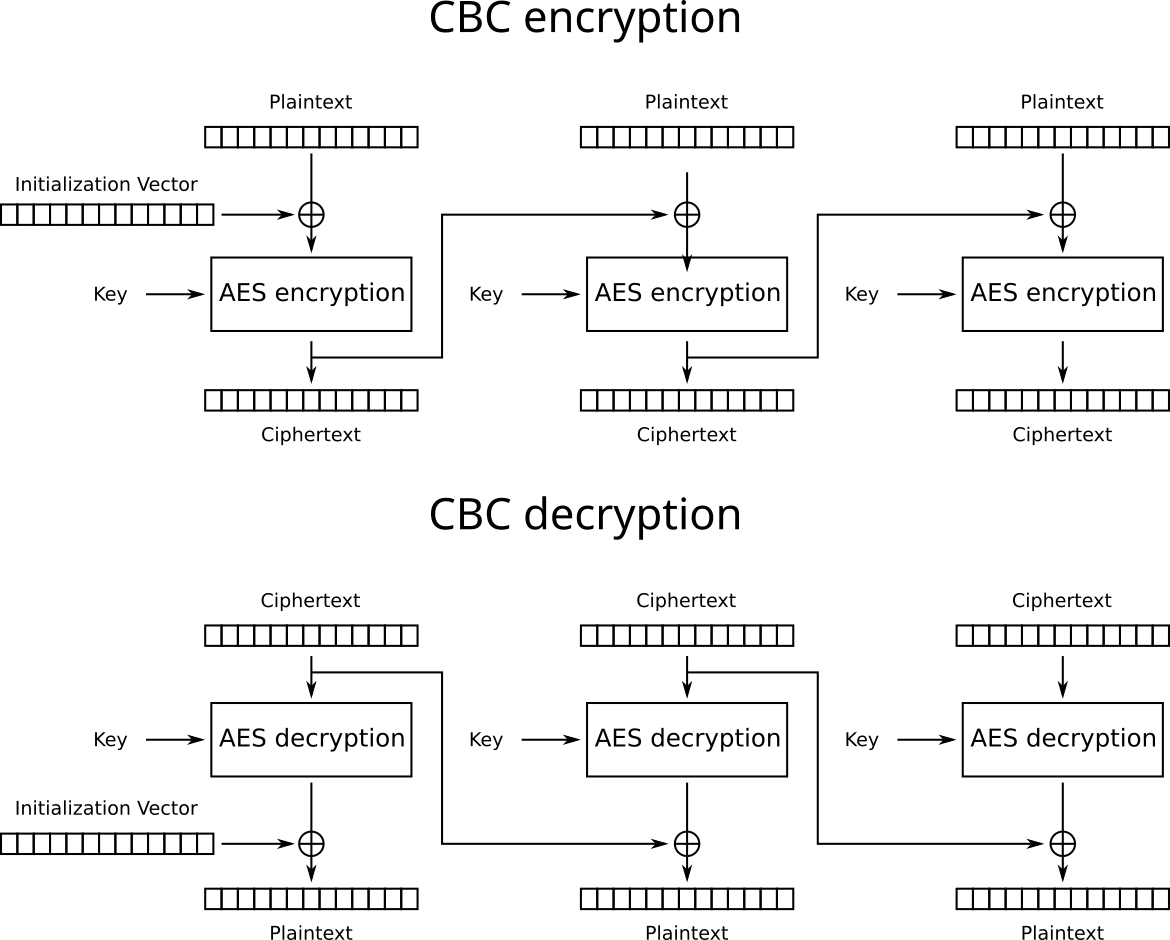
AES-CBC transformation scheme.
The IV acts as a randomization value (so ciphertexts are different, even if they contain the same plaintext) and as a source of issues. The IV should be random, unpredictable (but not secret) and differ from message to message, otherwise, some BEAST in the bushes could come and break your system.
But imagine that the IV is hardcoded and never changes, what can go wrong?
Besides the mentioned BEAST, the static IV also leaks repetition among the plaintexts, which is already some information that the encryption fails to hide.
For example, take a look at these records:
> 8713e3d410ea18378175d5b035881bf2c12ad5576b5e3c71c35fc7cf8de8326f8...
> 8713e3d410ea18378175d5b035881bf24c26fd0c6a7d3b19de2a8c5ffd0fda55e...
> b8bb05196d12fbb5c6b9352653b6caefa3090b02a528e138be27717e3af74b7ec...
> 8713e3d410ea18378175d5b035881bf20c93a925c12d3f26ca7618e4126959944...
> 8713e3d410ea18378175d5b035881bf25eb1881e23dbb0384f04fe834b99401fe...
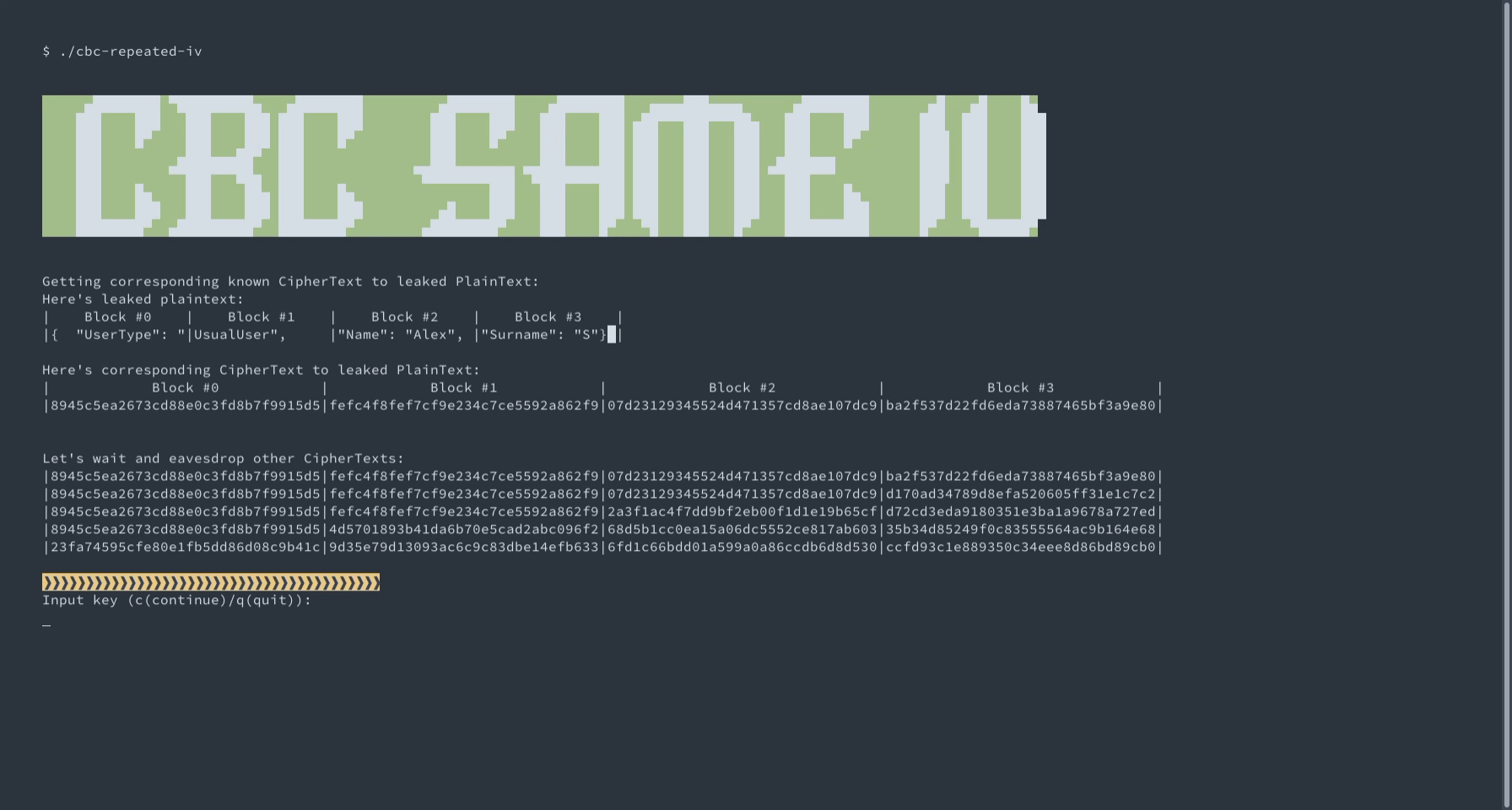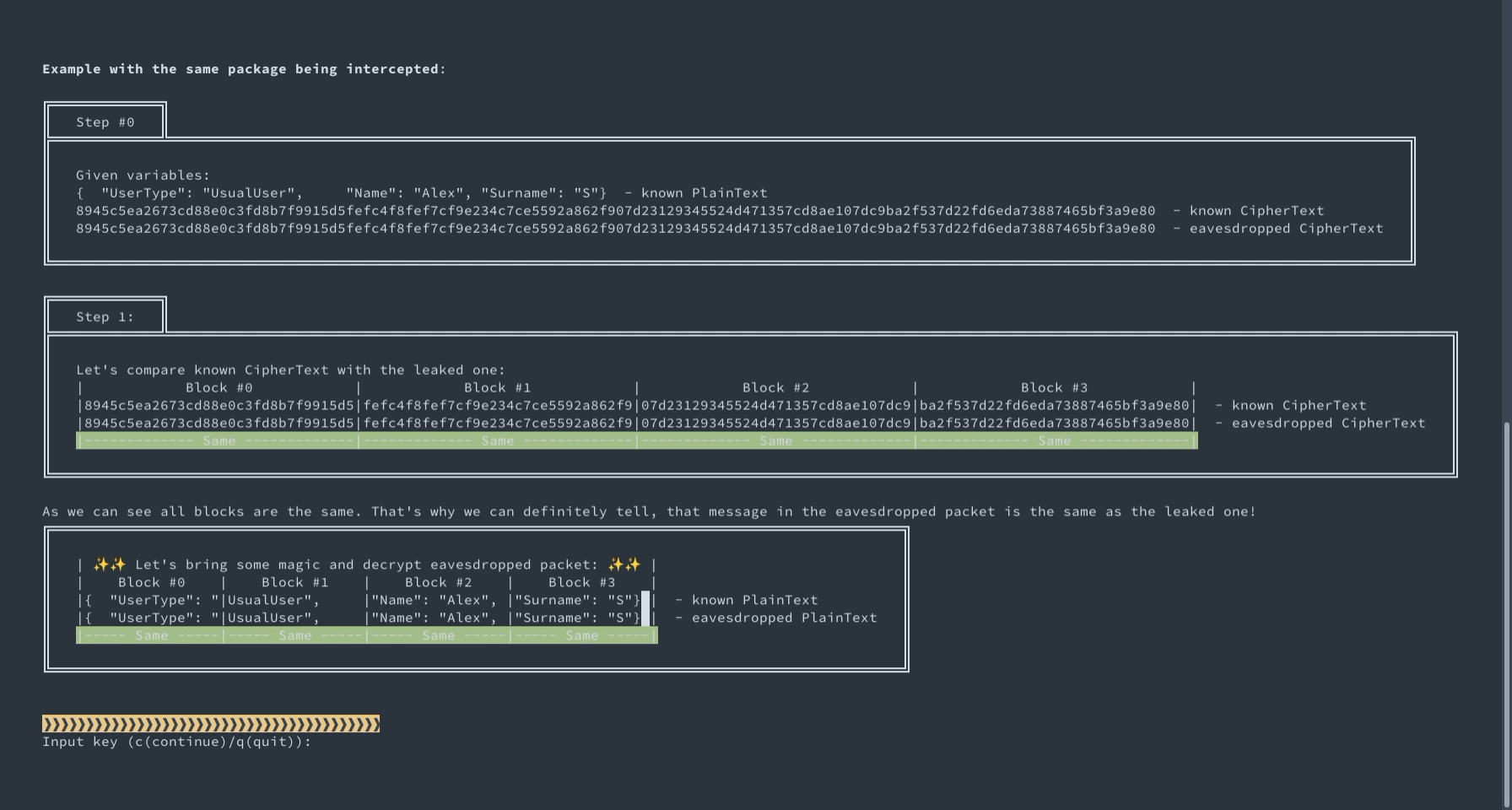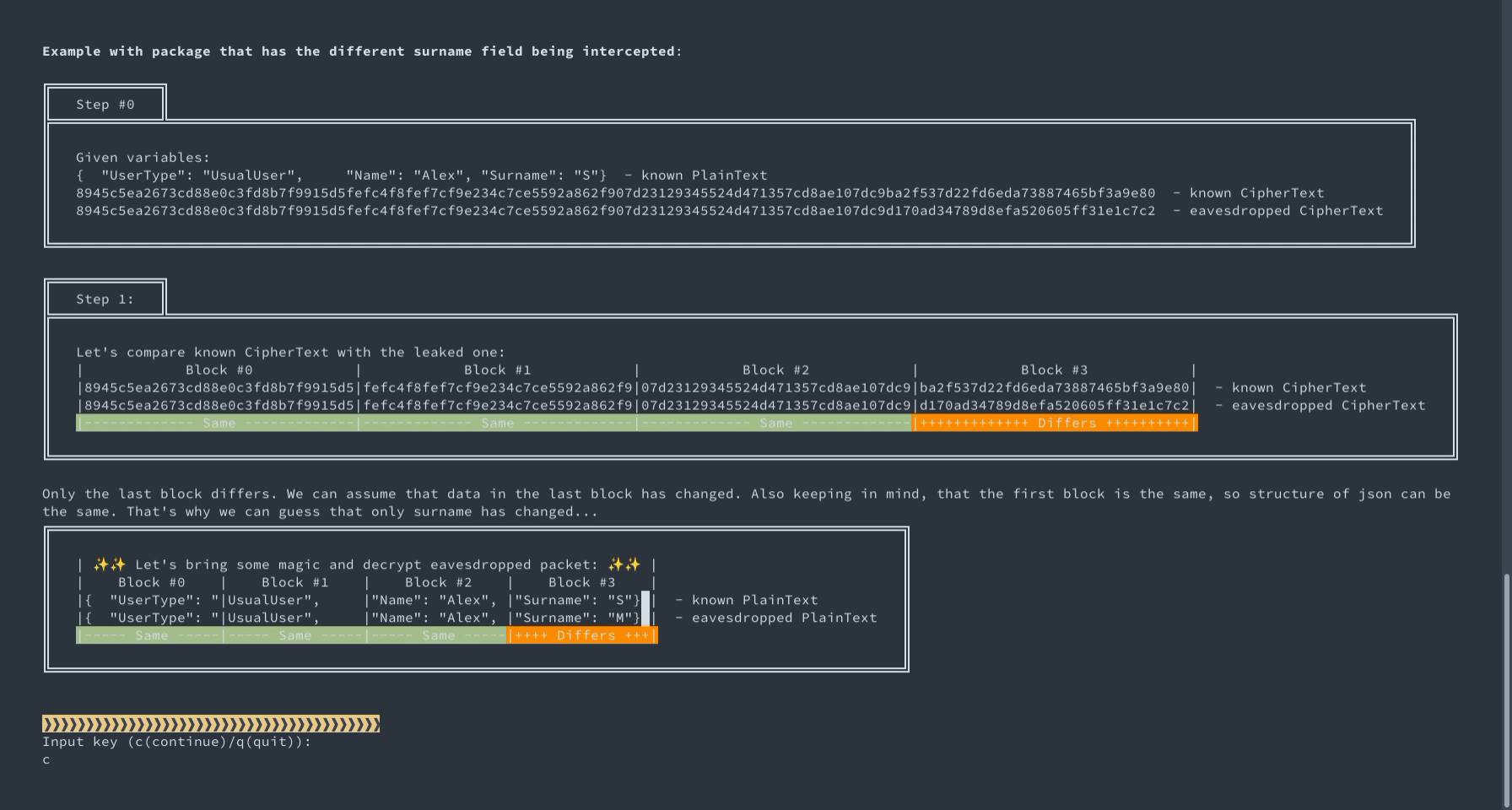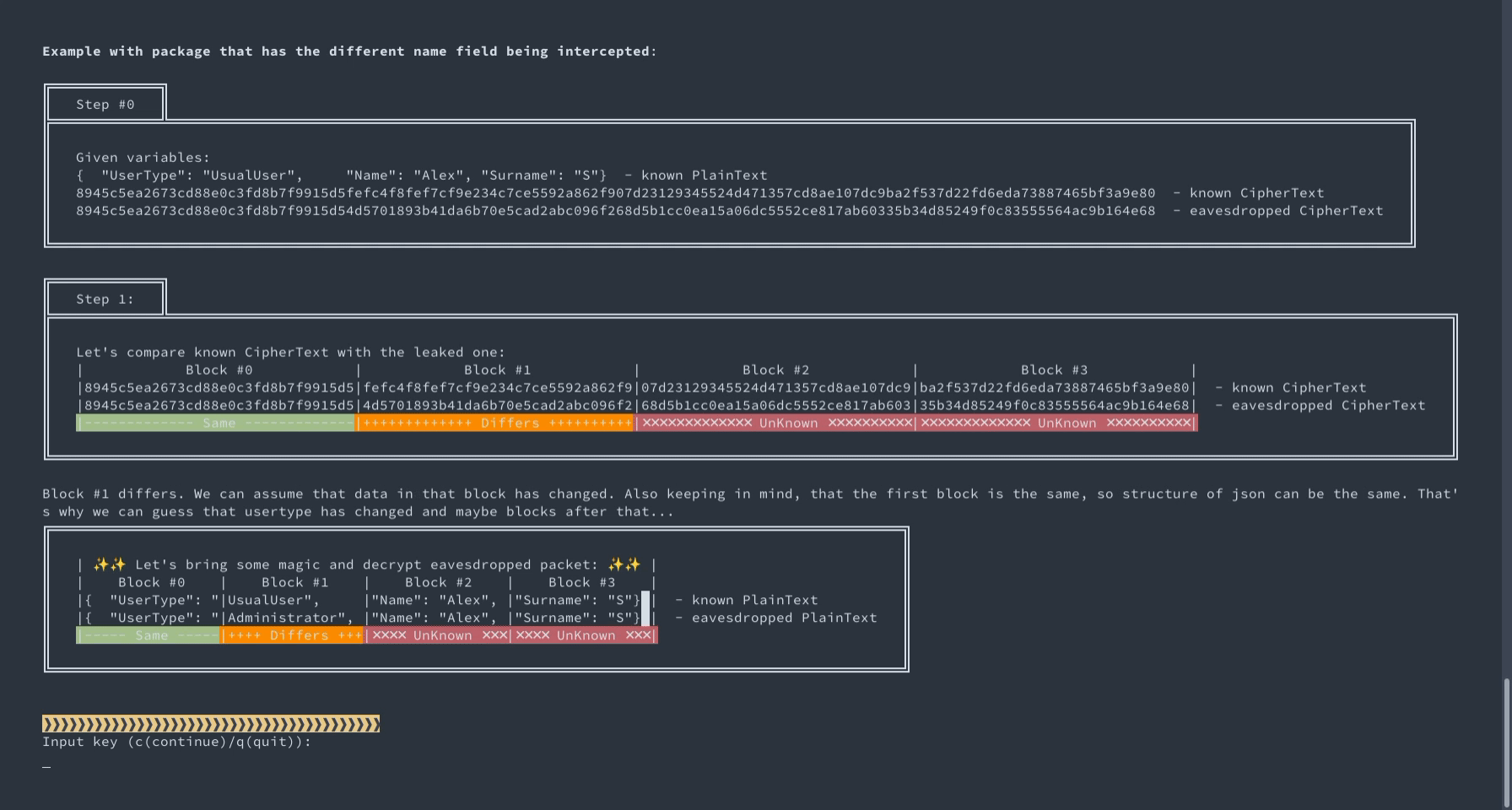
What if we tell you that these are the logs in JSON format, encrypted line by line in CBC mode with a static IV? Can you tell which logs have info level and which are errors? You can suppose that each log begins with {"level":"xxxx",...} and you will be 100% correct. This is just an example, one among many, of why encryption must be probabilistic and how static IV in CBC fails to achieve it.
Static IV demonstration #
We’ve prepared a demonstration of static IV in AES-CBC. This is an interactive demo that leads you through several examples and shows how to get some basic knowledge about ciphertexts encrypted with the same IV.
Interactive demo of using repeated IV in AES-CBC
An interactive demo of intercepting and decrypting data encrypted using AES-CBC and static IV.
This demo shows how the repeating of init vector can be dangerous for the sake of data security. To be exact, it shows how ciphertext would change or not :) while reusing vector in CBC mode. To be more authentic in our example, we show some simple cases with small JSON packets. Also, cipher and plain texts are separated in blocks by 128 bits. It helps better understand which and why one block differs and the other correspondingly stays the same.
Also, the Replay attacks can be considered as a threat to the CBC init vector reusing vulnerability.
How to prevent a static IV mistake? #
Always read and follow the original security requirements of the primitives. If the IV should be unpredictable, make it unpredictable. If the nonce should be used once, use them only once. If you don’t know how to fulfil all these requirements—hire someone who can.
Using static IV itself is not a “terrible” thing, but typically it’s a stepping stone for more powerful attacks. See also CWE-329.
Exploiting AES-CBC Padding Oracle attack #
Have you ever played Wordle?
It’s a game where your task is to guess a 5-letter word. You can submit words of the same length, and the computer will tell you when the letters are matched or occupy the correct spot.
Suppose there is another game, call it Cryptle :).
In this game, the computer generates a plaintext of some structure, encrypts it, and gives the result to you. You can somehow tweak the ciphertext and send it to the computer. After the decryption, the latter will tell you some information about the decrypted plaintext’s structure, for example, if it’s valid or not. Your task is to decrypt the message.
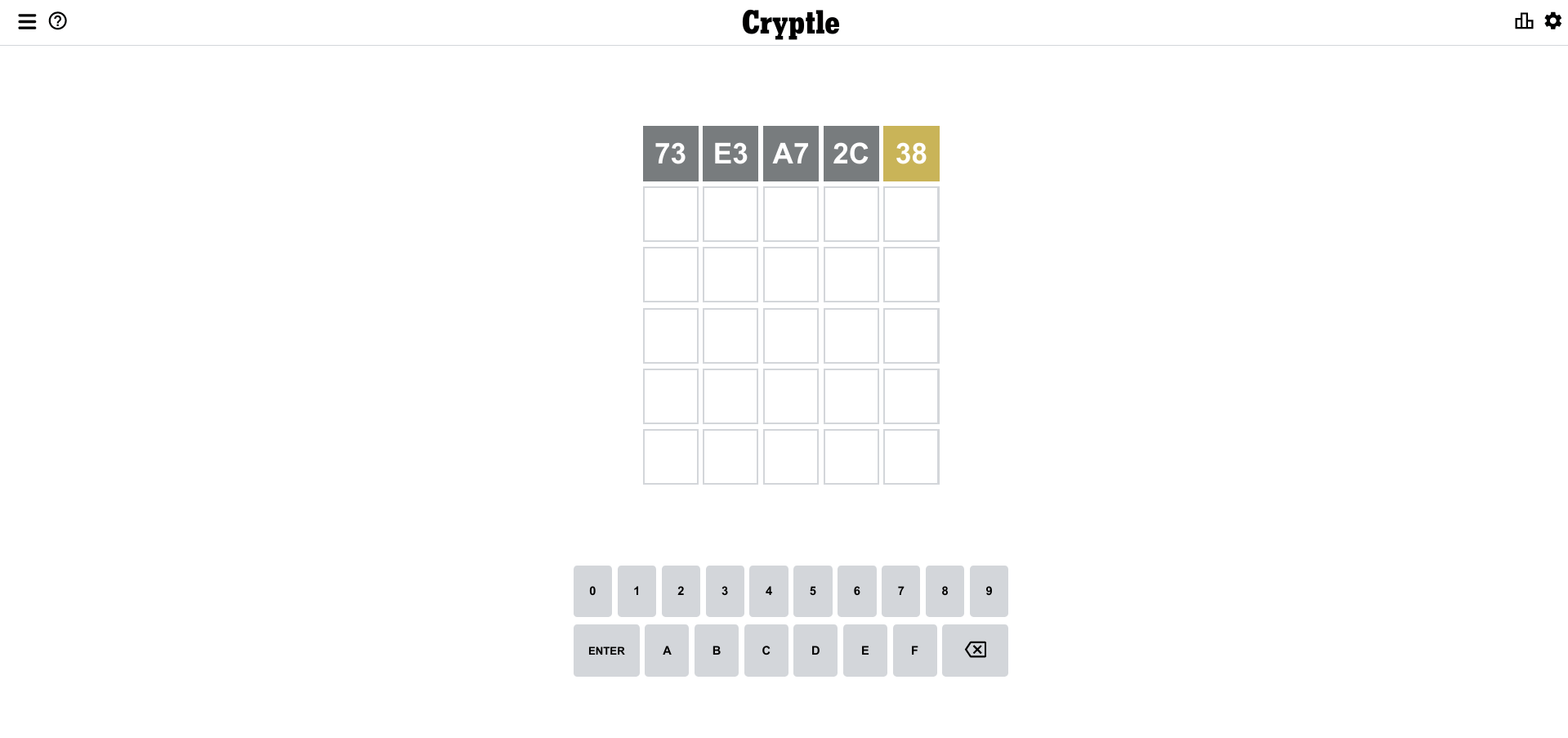
Let’s play Cryptle – a cryptographic Padding Oracle game!
Depending on the structure and the type of the given information, by making an appropriate number of queries, you can always win this game. This is what oracle attacks are in their heart.
An oracle is an abstract machine that can answer some questions. Such oracles can naturally come up in complex enough systems. For example, there could be places where someone submit a ciphertext, and the system somehow signals whether this ciphertext decrypts correctly or not, acting as a decryption oracle. It could be as simple as either returning an error to the user or writing error logs, or strange behavior in the protocols’ execution. Even the difference in processing time is enough. This is what we call a leakage, and attacks that exploit it are called side-channel attacks.
Let’s return to the CBC. To protect innocent toy cars, we will avoid exact examples and just give a general overview of what goes wrong. Almost all block-based ciphers use some kind of padding for the last block. The CBC uses PKCS#7. The idea is to append n bytes, each of which is n, to make the length nearest multiple of block size.

PKCS#7 padding scheme for AES-CBC.
The CBC mode is malleable—an adversary can modify the original ciphertext in a way that the decrypted plaintext will change predictably. Specifically, the adversaries can flip bits of one cipherblock, which will flip bits in the next plaintext after the decryption. They can start to mess up with bits and modify them in a way that triggers padding validation or invalidation in the last block.
If the adversary can produce the correct padding, for example 02 02, and the system signals that the ciphertext is indeed valid, then they will automatically know the last two bytes of a plaintext, just by solving a simple equation:
plaintext xor iv = "02 02"
Where:
- plaintext — unknown
- iv — controlled by the attacker
02 02— known to the attacker (thanks to the oracle)
So, by rearranging:
plaintext = iv xor "02 02"
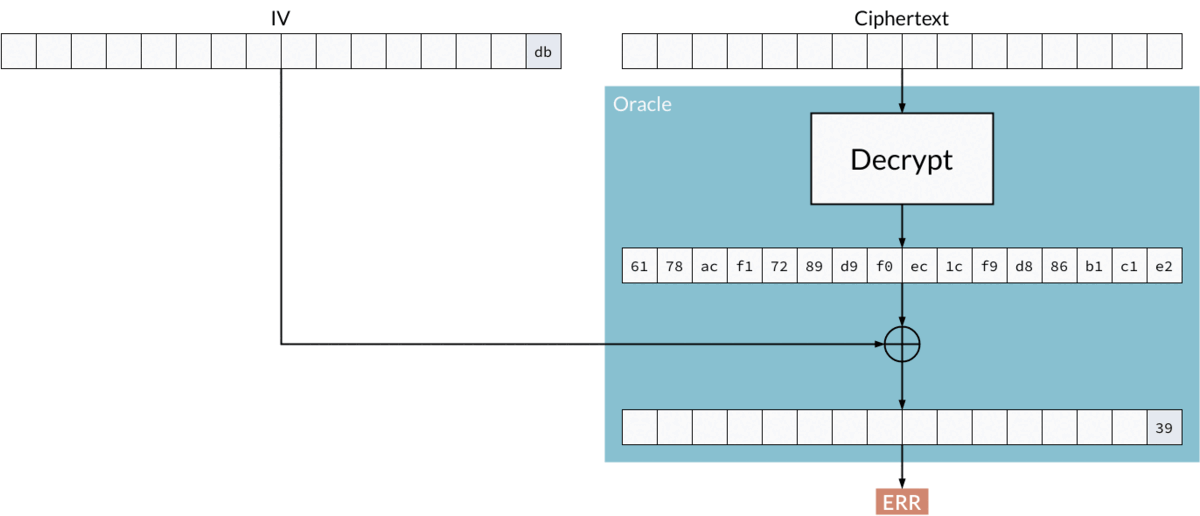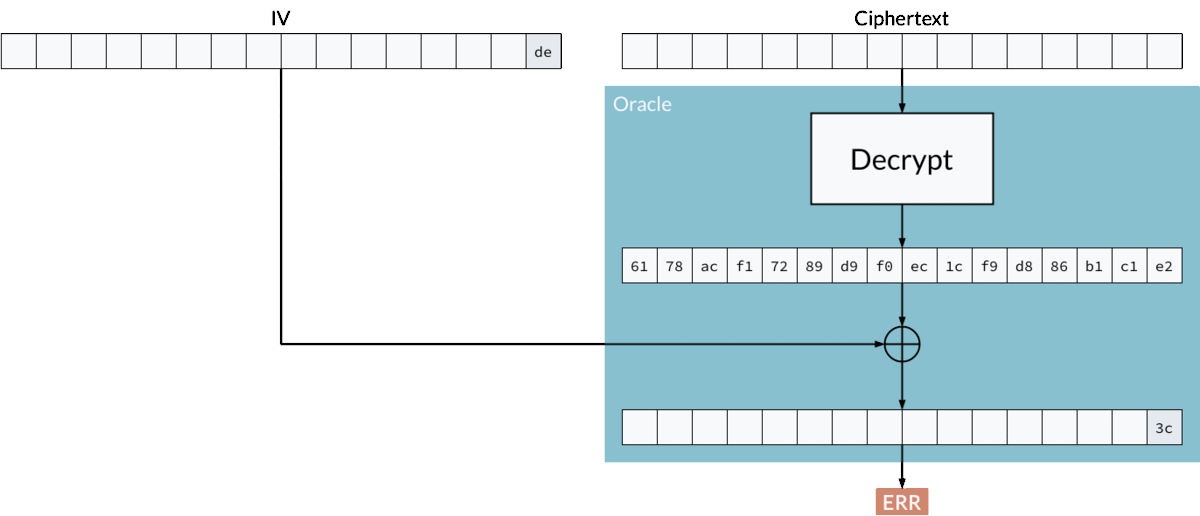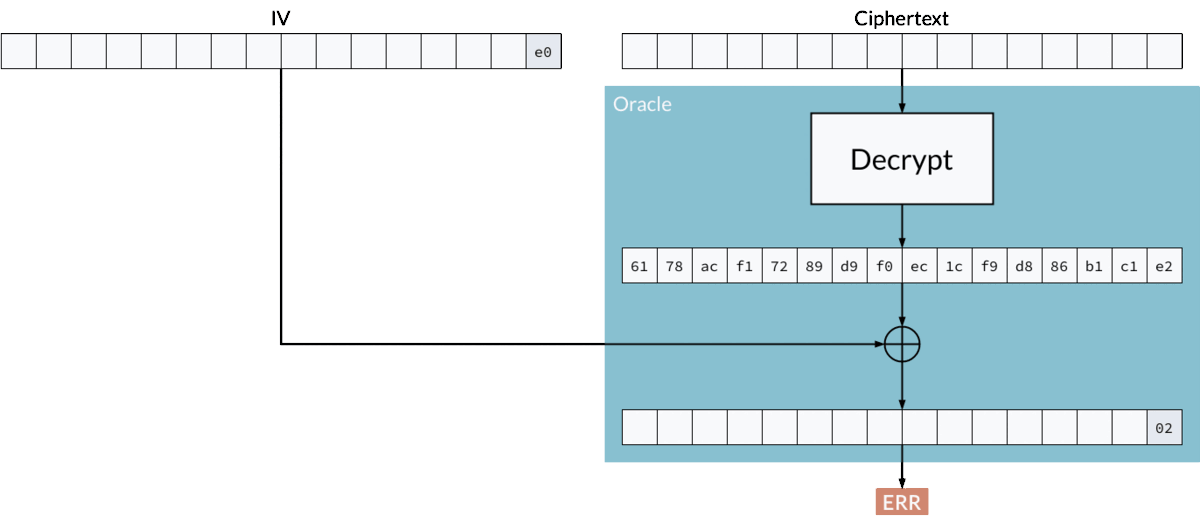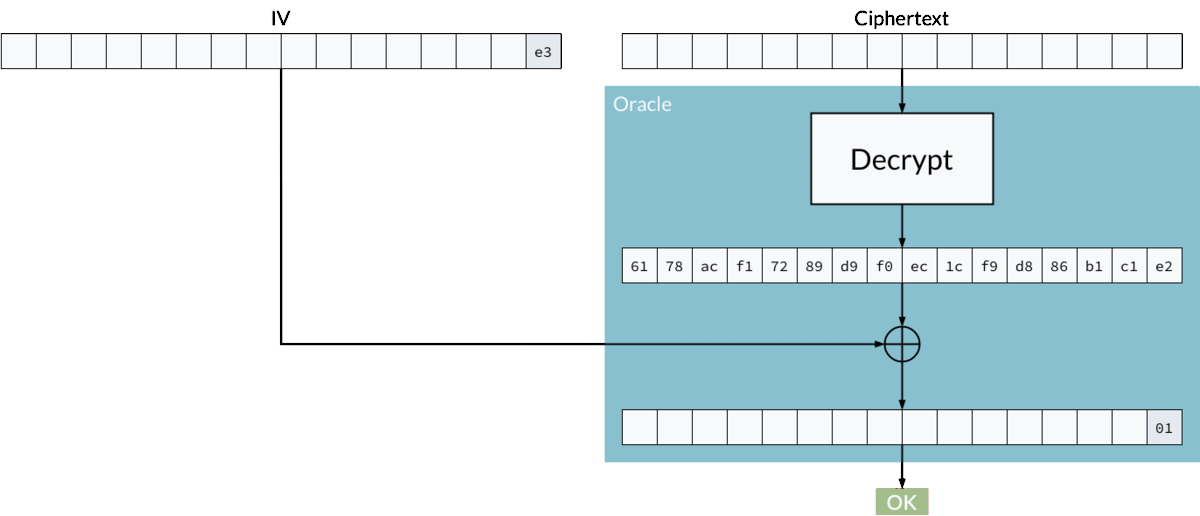
Finding the last byte using padding oracle attack.
In this way, byte by byte, the adversary can recover the whole plaintext without knowing the key.
Padding Oracle attack for AES-CBC demonstration #
We’ve prepared an interactive technical demonstration of this attack. You can see there step by step how the oracle can help recover the plaintext without the key.
Interactive demo of exploiting Padding Oracle in AES-CBC
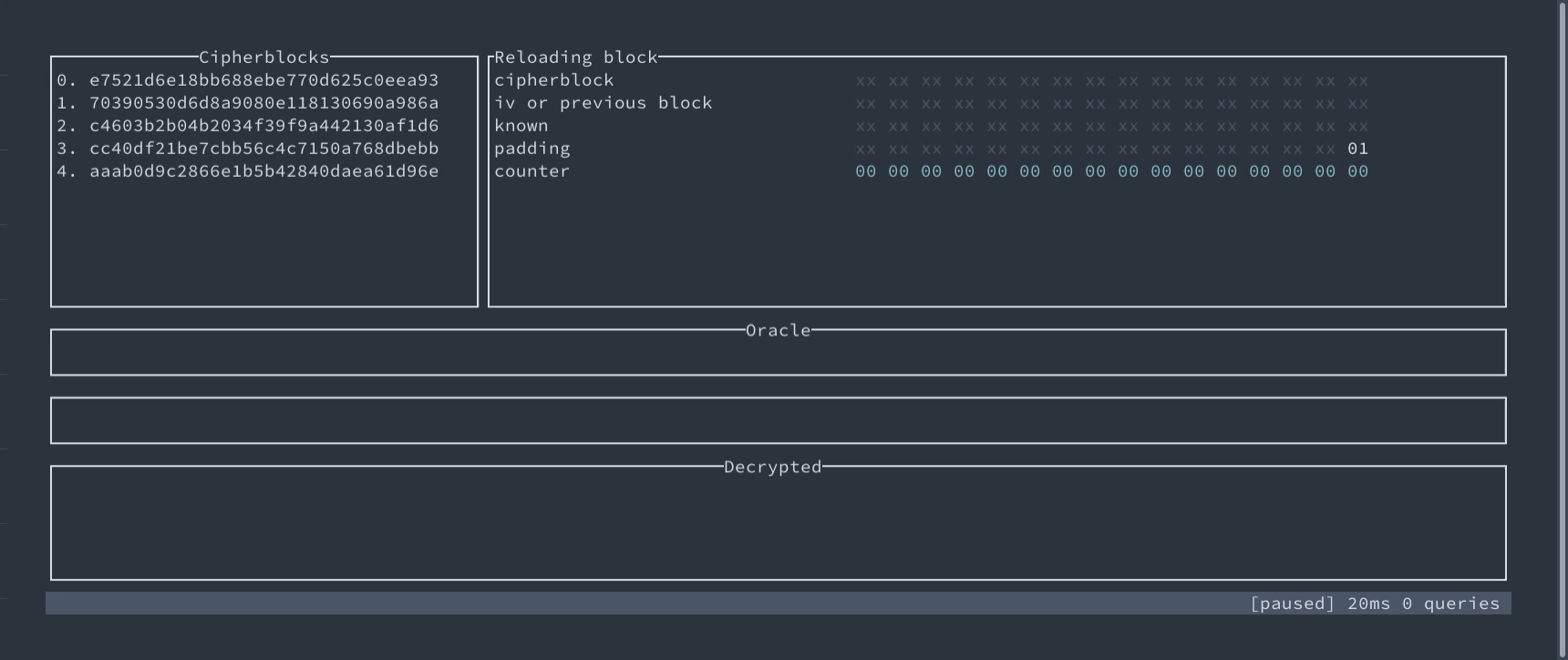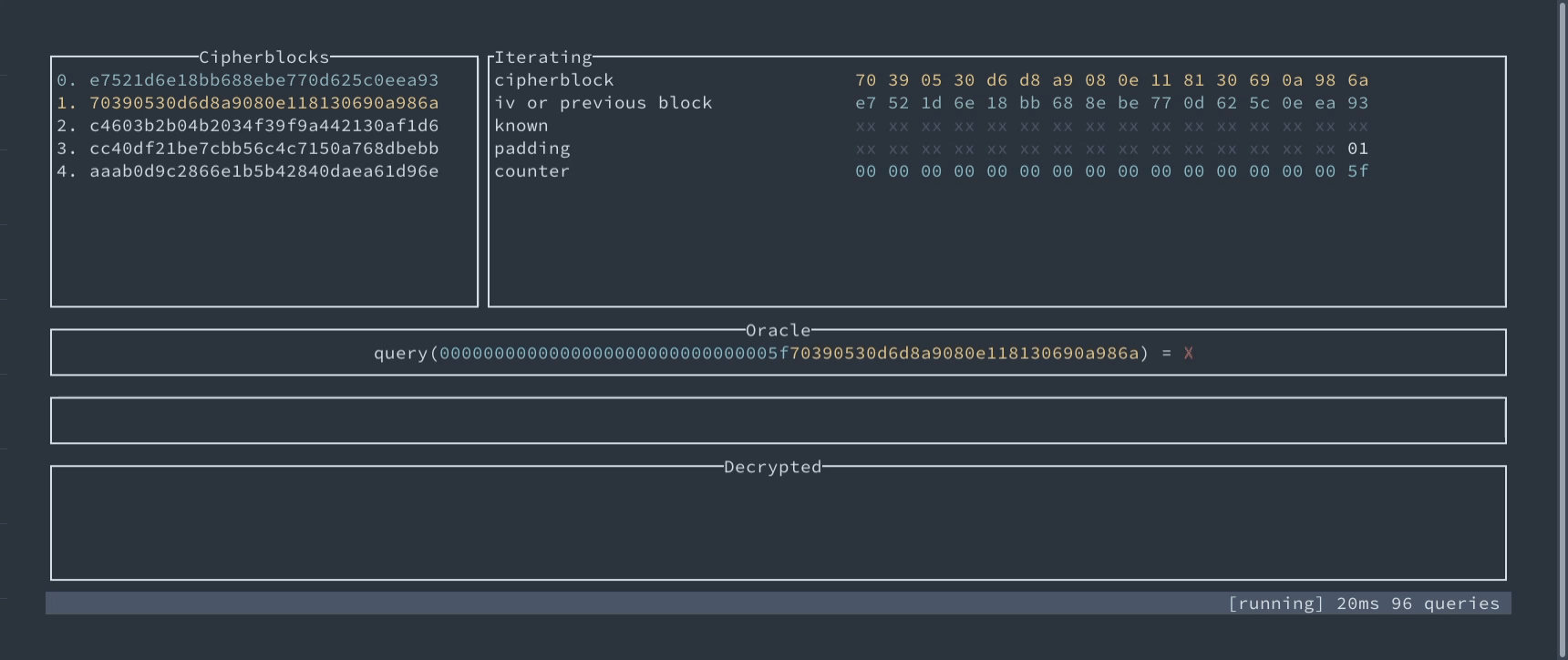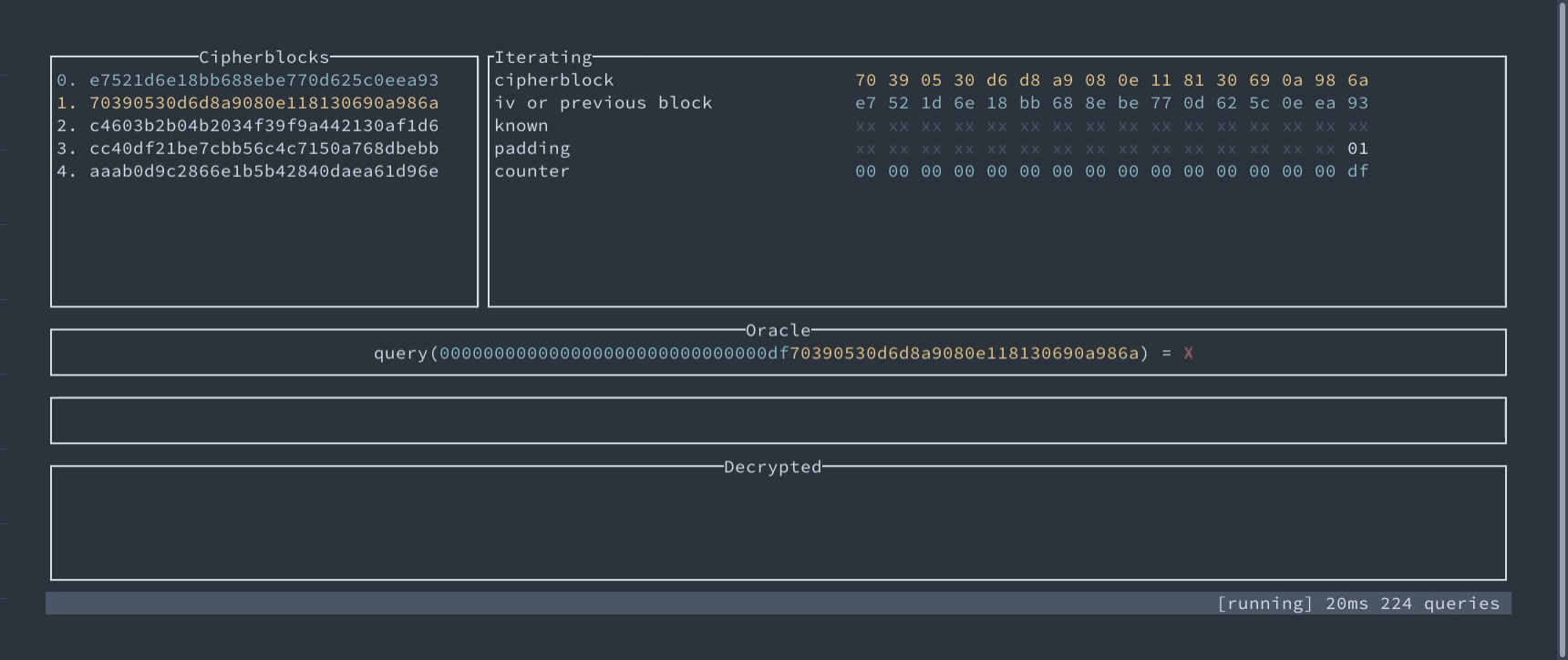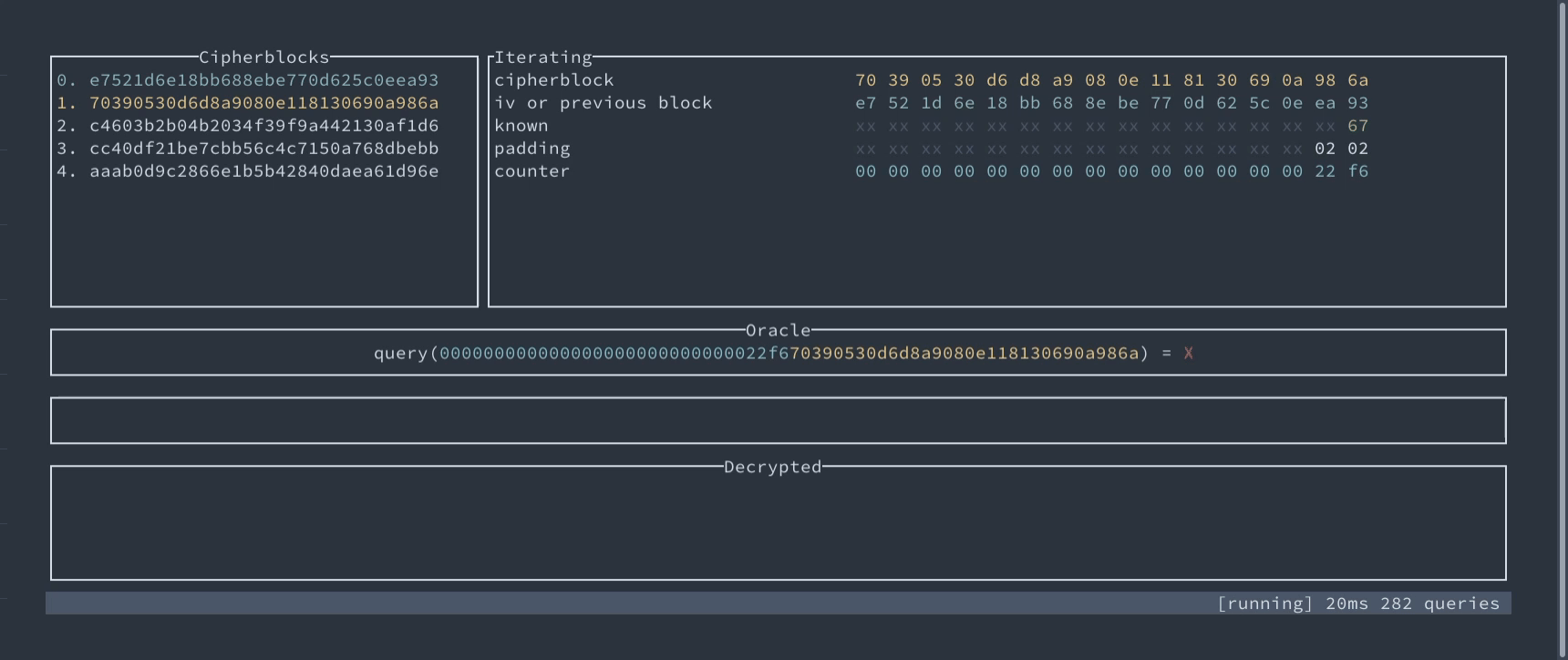
An interactive demo of Padding Oracle attack – find and decrypt secret byte-by-byte.
In some cases, even if the cryptographic code is not susceptible to padding oracle, the leakage could occur on a higher level—on a transmission protocol, for example. No one is safe from Padding Oracle attacks!
How to prevent Padding Oracle attacks? #
Always use integrity checks, verify them before any other operation (otherwise you’ll have a chance to play a cryptographic doom), and don’t forget about constant time comparisons (time leaks are another kind of side-channel leaks). In general, audit your code and use authenticated cipher mode, like AES-GCM, instead.
Breaking AES-CTR with fixed nonce #
Let’s return to the CTR, a second encryption mode available in toy cars.
The CTR is a beautiful way of transforming a block cipher into a stream one. All stream ciphers, beside the key, require a randomization value called nonce. The name implies that this value MUST be used only once. That’s where the best part of the audit lies.

AES-CTR transformation scheme.
Stream ciphers work in the same way: to encrypt a bit a they generate a pseudo-random bit k and XOR these two together. The k is either 0 or 1 with a 50% probability each, which means that the value a xor k would be 0 or 1 with 50% probability each as well, regardless of the value of a. The k “hides” the bit a, therefore, the resulting ciphertext always looks like a random string.
The decryption is applying the same operation: because of the XOR properties that x xor x = 0 and 0 xor x = x, the decryption goes as (a xor k) xor k = a xor k xor k = a xor 0 = a.
The CTR mode is secure and efficient. It allows parallelizing computations, doesn’t require padding, and can be precomputed (the keystream requires only the key and nonce). Unfortunately, it breaks drastically when misused.
Suppose there are two bits, encrypted with the same key: k: a xor k and b xor k. Let’s XOR them and see what happens:
(a xor k) xor (b xor k) = a xor b xor k xor k = a xor b
Oops, the k disappears as its hiding property, and we are left with an XOR combination of a and b.
The nonce is used to ensure that the stream of k’s is different each time, even when messages are encrypted with the same key. Nonce is not required to be unpredictable as well as secret, but it MUST NEVER be reused with the same key (see NIST SP 800-38a).
In the original code, not only the nonce was reused, but worse, it has never changed, there is no way of doing that.
Let’s look at a practical example of what can go wrong.
Suppose there is an HTTP GET request that is encrypted by the same protocol as we described above:
GET /user/auth/login HTTP/1.1
Authorization: Basic XXXXXXXXXXXXXXXX
Accept: application/json
First, it would be split into two 48-byte packets:
GET /user/auth/login HTTP/1.1\nAuthorization: Bas
ic XXXXXXXXXXXXXXXX\nAccept: application/json
Then, each part will be encrypted with the same key and nonce:
d3ade77ff91c6991c2b211ba1d152c52e8b958e32c6b891f2ef45b440d9a02df279296f28b7cf2c3079771b8bb833f8c
fd8b9306e450609782db1aae130d7067d0944b874d40be2e0eaf504a5de033c63a9998f48b69fd98048b70ec91
As an attacker, we can xor these two pieces together:
d3ade77ff91c6991c2b211ba1d152c52e8b958e32c6b891f2ef45b440d9a02df279296f28b7cf2c3079771b8bb833f8c
xor
fd8b9306e450609782db1aae130d7067d0944b874d40be2e0eaf504a5de033c63a9998f48b69fd98048b70ec91
=
2e2674791d4c090640690b140e185c35382d1364612b3731205b0b0e507a31191d0b0e0600150f5b031c01542a
We got a XOR combination of the plaintexts of the first and the second packets. How do we know? Well, let’s XOR them and see:
"GET /user/auth/login HTTP/1.1\nAuthorization: Bas"
xor
"ic XXXXXXXXXXXXXXXX\nAccept: application/json"
=
2e2674791d4c090640690b140e185c35382d1364612b3731205b0b0e507a31191d0b0e0600150f5b031c01542a
The resulting value is the same as when we XORed the ciphertexts. Cool, isn’t it? Now, let’s get the token. By rearranging the last equation, we get:
"GET /user/auth/login HTTP/1.1\nAuthorization: Bas"
xor
2e2674791d4c090640690b140e185c35382d1364612b3731205b0b0e507a31191d0b0e0600150f5b031c01542a
=
6963205932397a6332466a617a707359574a7a0a4163636570743a206170706c69636174696f6e2f6a736f6e0a
As an attacker, we can do it because the login request is the same for every user, except for the token. Meaning, that attackers know the plaintext of the first packet, as it doesn’t include the varying part.
Let’s decode the resulting string:
hex::decode(6963205932397a6332466a617a707359574a7a0a4163636570743a206170706c69636174696f6e2f6a736f6e0a)
-> "ic Y29zc2FjazpsYWJz\nAccept: application/json"
Bingo, we’ve found the token!
This is just a simple example, but it is not very different from the real world. If nonce is reused, the task of decrypting the messages becomes a puzzle in the Sunday newspaper instead of a computationally infeasible problem.
By the way, the wittiest thing was the comment above the hard-coded nonce:
// Temporary solution. These values should be provided by the user.
The line was added 6 years ago.
Capture-the-flag breaking AES-CTR with fixed nonce #
Here’s a demo game for you! Retrieve the flag value from eavesdropped ciphertext and submit it.
This example covers unknown ciphertext decrypting—one of two vulnerabilities of using CTR with the same nonce. A curious reader can notice that in this demo we’re XORing the flag value with other different hex values. This second value, in fact, is a stream CTR key (don’t confuse it with AES cipher key), which can be used to decrypt/encrypt any custom plaintexts, shorter or equal to the byte size of the retrieved stream CTR key. All this happens below the target’s radar.
Demo of decrypting AES-CTR with a reused nonce
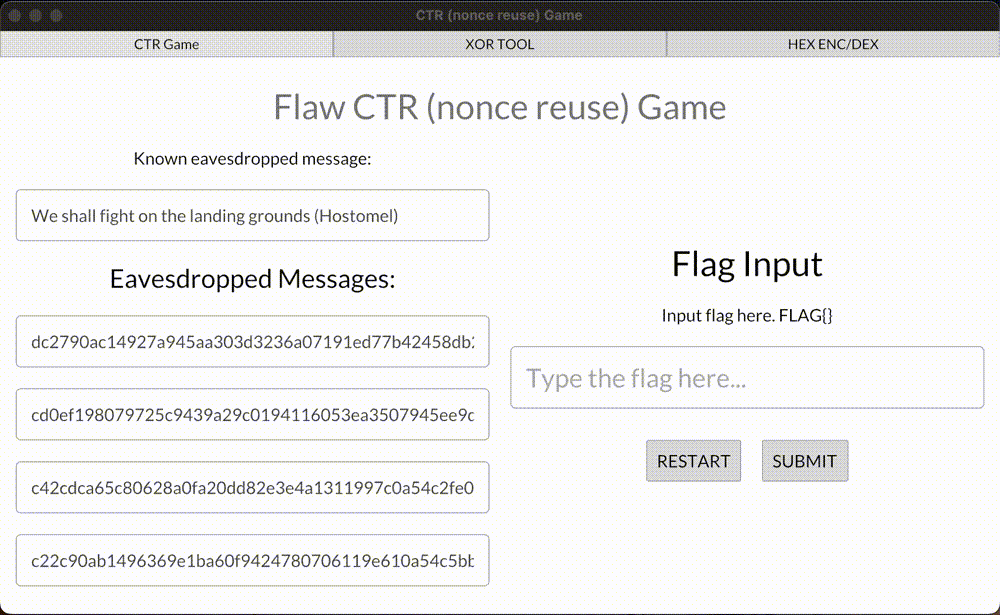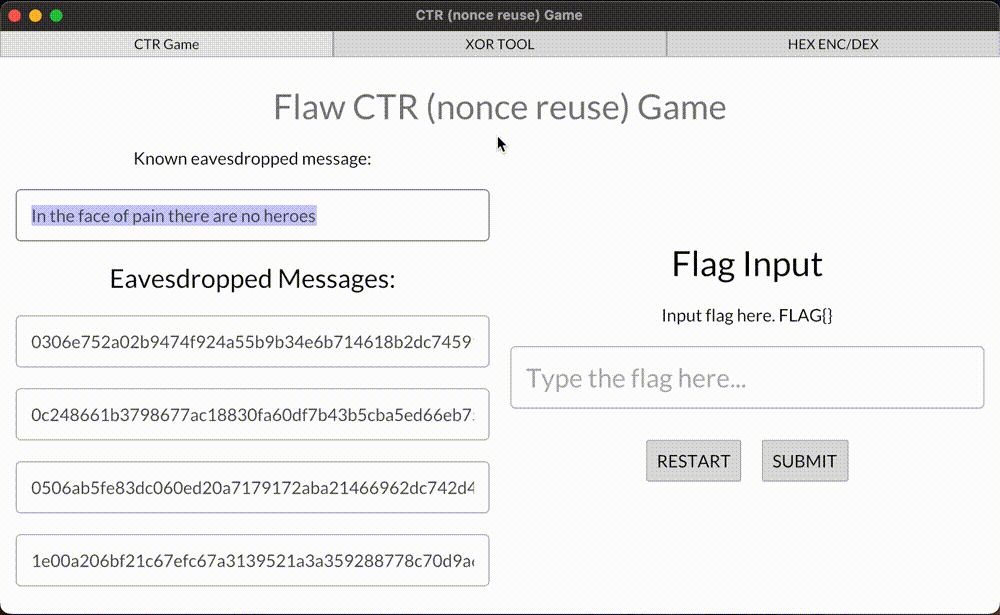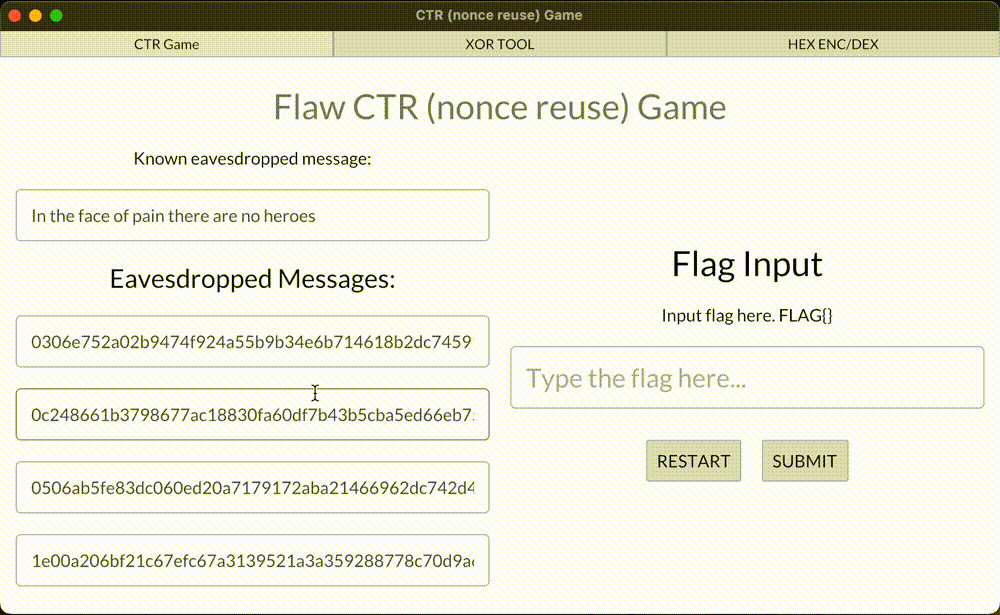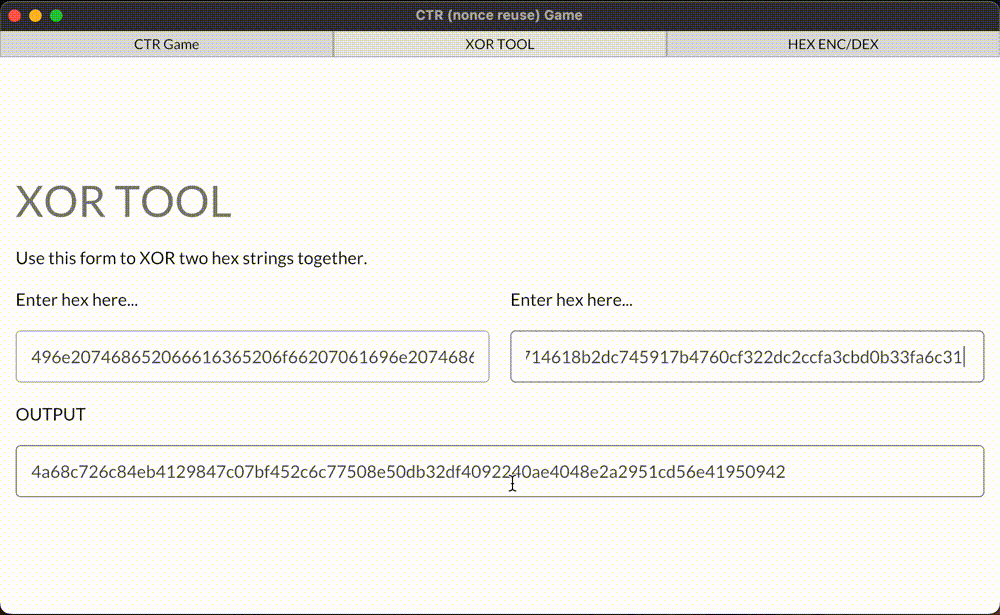
A demo game of decrypting flaw implementation of AES-CTR ciphertexts because the nonce value was reused.
Remember when we said the CBC was malleable? Well, it’s nothing compared to CTR!
Even on correct (sic!) implementation of CTR with non-repeating nonce, but without integrity guarantees, an adversary can change individual bits of the plaintext with no traces at all. With such (raw) power, your secret messages (or naughty photos) to “recipient: BOB” may unexpectedly come to “recipient: EVE”.
Non-existing integrity protection for CBC and CTR #
Let’s return to our packets. We’ve said that the packets consist of an encrypted payload, the length, and a checksum. The last implies that integrity is guaranteed—does that mean that some of the attacks described above are not possible? Well, think again because the authors of the toy car crypto-system have selected CRC-16 as a checksum algorithm!
Okay, what is integrity? In simple words, message integrity is a guarantee that the message wasn’t changed by something (random noise or the will of the Universe) or someone (an adversary). If the message was changed, the integrity check let us know.
The resistance to the forces of the Universe can be guaranteed by a simple error correction code (spoiler: this is what the CRC is), but the latter property requires a secret key to keep the integrity check unforgeable for a clever humanoid.
As you’ve probably guessed, the CRC doesn’t accept a secret key. So, anyone can forge it!
You can even try it in our demo! Your task is to use the malleability of the CTR mode to encrypt a custom message. But the ciphertext is protected by the CRC-16 tag. Thus, you should forge it as well.
Interactive demo of changing AES-CTR encrypted messages
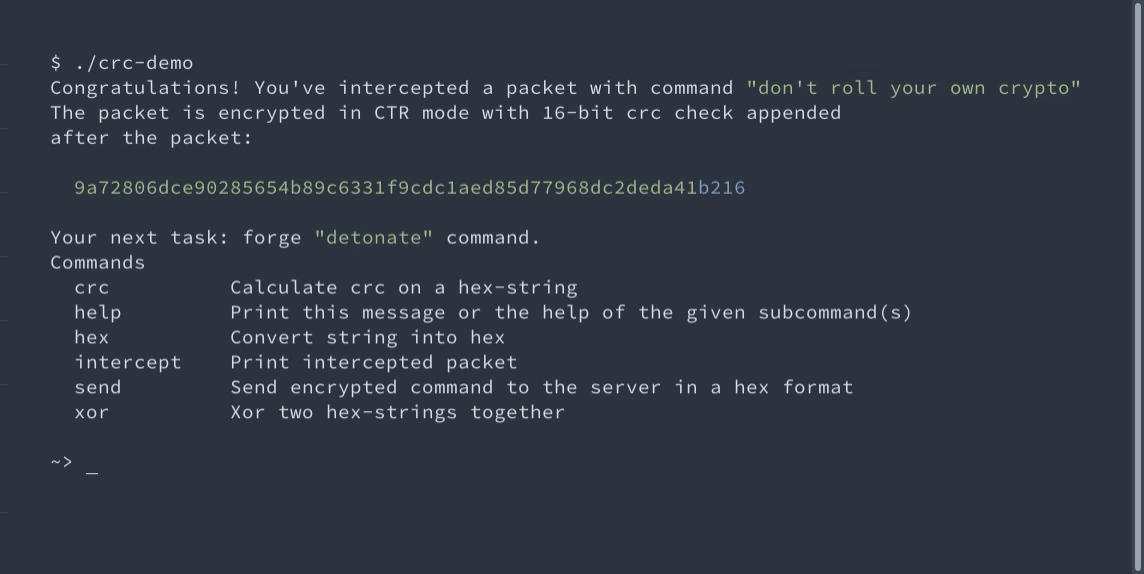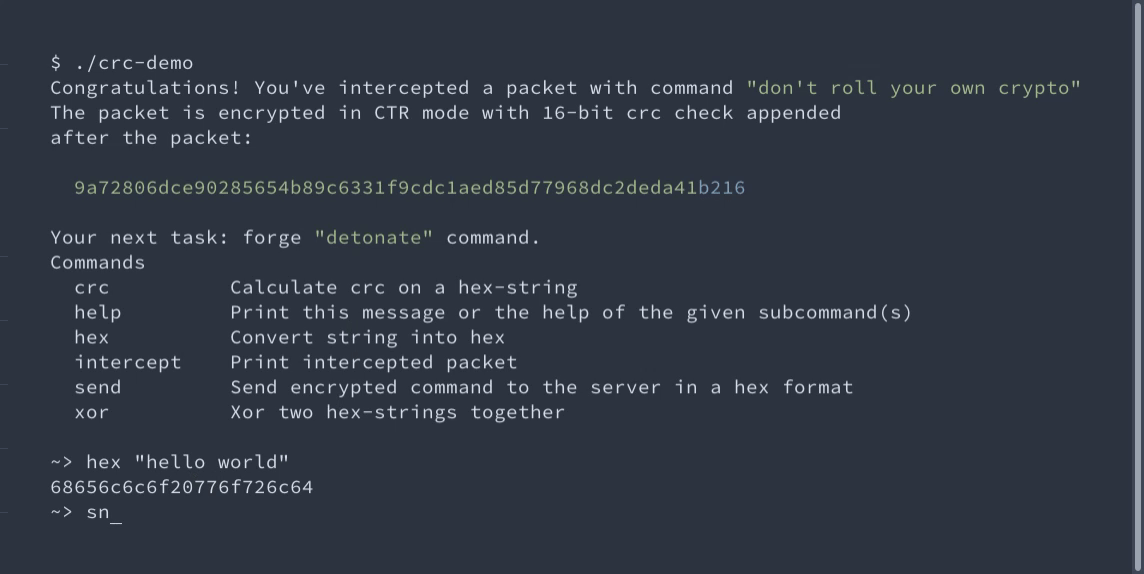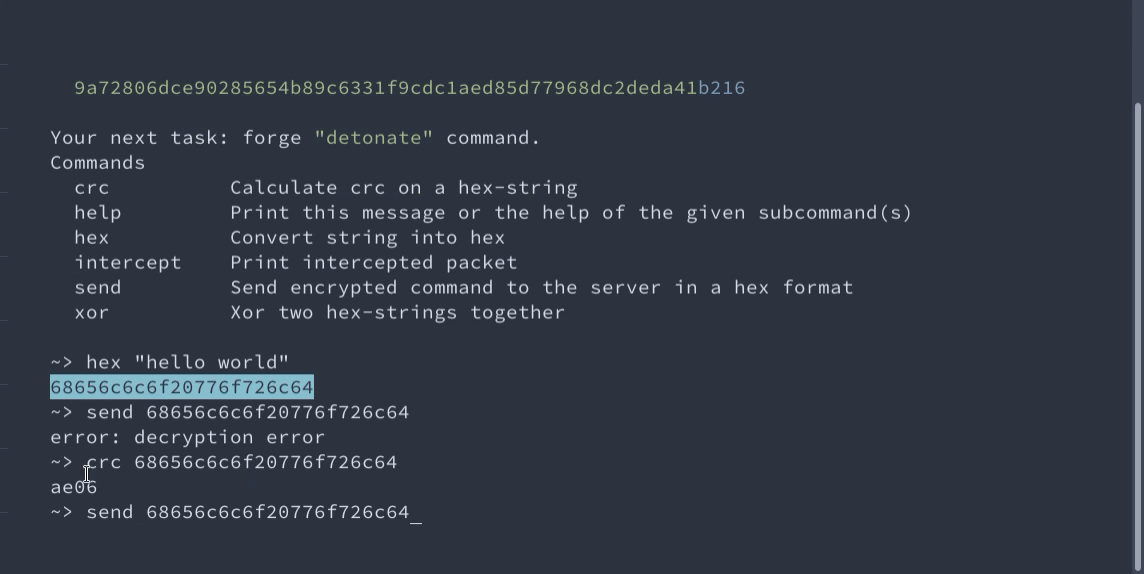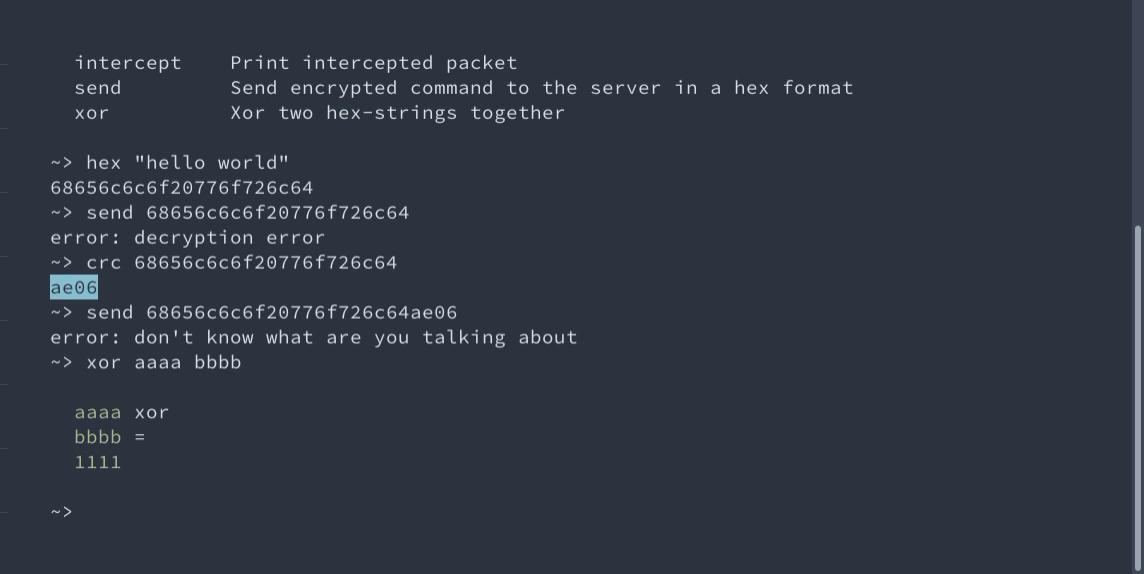
An interactive demo of unnoticeably changing AES-CTR messages because CRC should not be used for integrity.
Besides, take a look at pseudocode that inherits the main idea from the real one:
if use_encryption:
ciphertext = encrypt(data)
tag = crc(ciphertext)
packet = concat(ciphertext, tag)
transmit(packet)
else:
transmit(data)
This code clearly indicates that the tag is used as a cryptographic integrity mechanism, not just as a fancy check.
Ok, let’s assume that instead of the CRC16, there is some proper integrity mechanism, but the length is still 16 bits.
Forging 16 bits by luck is a matter of time: probability is 2-16 , or 215 (32768) tries on average. With the ability to send thousands of messages per second, it’s nothing, and if you only need to forge one or a couple of messages to break the system, it’s worth doing even for millions of them. The system grade tag size standard is at least 96 bits (as in AES-GCM) or better 128 bits (as in ChaCha20-Poly1305).
How to protect integrity? #
The real solution, of course, is to use MAC: they are created specifically for these purposes!
If you are using the AES-GCM, the MAC is already built into the encryption/decryption itself (that’s why it’s called authenticated encryption). But the good idea is to use a library that chooses all cryptographic stuff for you and exposes only two functions: encrypt(key, message) and decrypt(key, message) just like Themis does, so, you can care more about other things in life than selecting integrity check function.
Replay attacks #
Another thing that often goes hand in hand with integrity is replay attacks.
Replay attacks are very simple: an adversary can passively listen to the traffic and capture packets to send these packets again later. Typically, replay attacks are used for denial of service, or triggering some processing again (like performing a money transaction twice, or moving the toy car further to the cliff), or in combinations with other attacks to KRACK the system.
If you want to try to exploit these attacks, we’ve prepared a game for you. Your task is to gain control of the enemy’s robot, which uses authenticated encryption to communicate with the enemy’s center, so forging the packets is infeasible. But you already know where to look at…
Interactive demo of replay attacks allowing to control robotic device
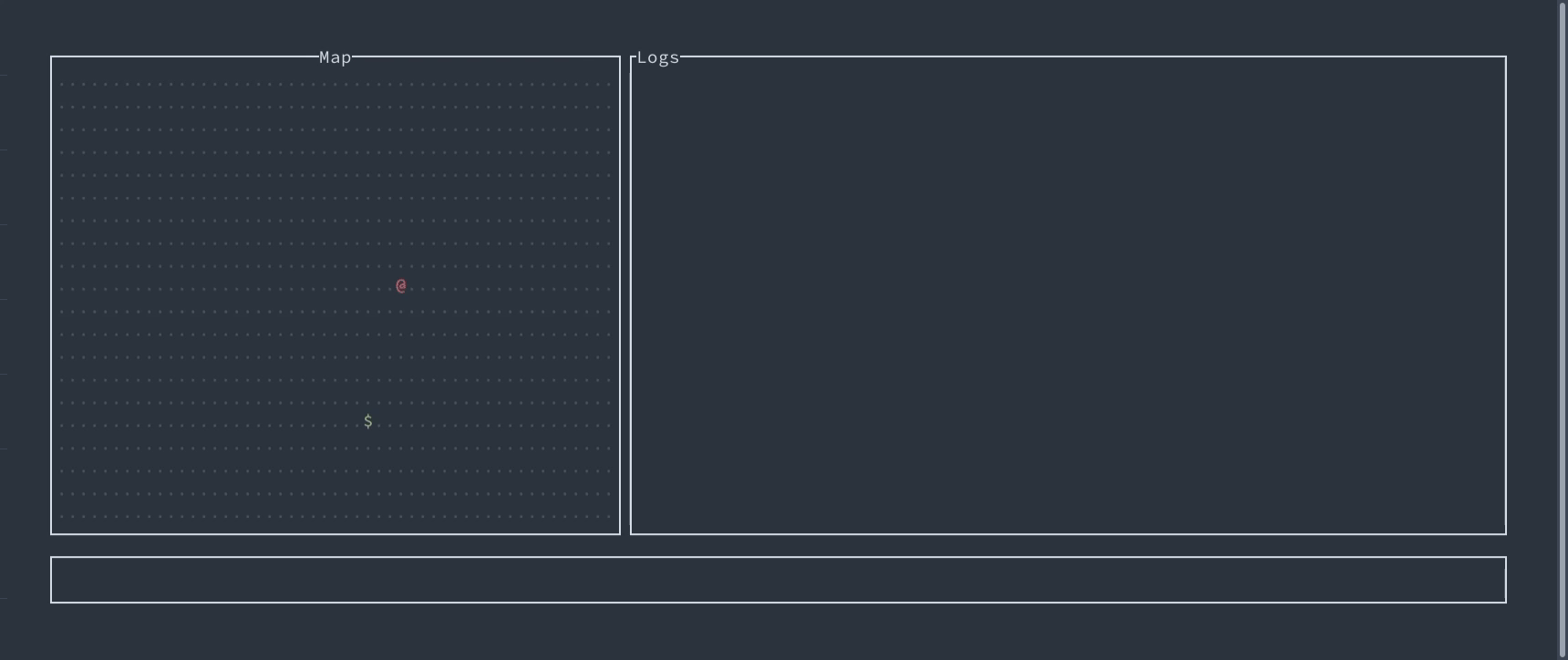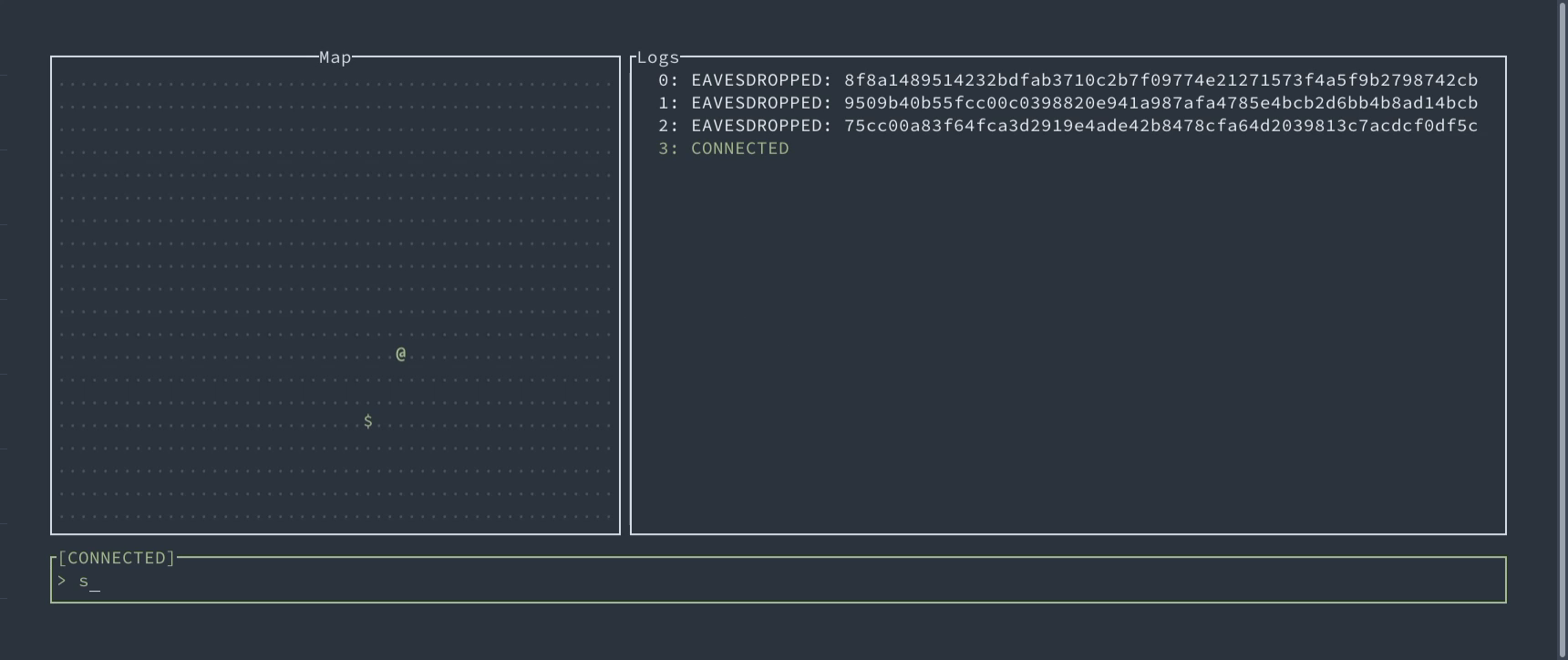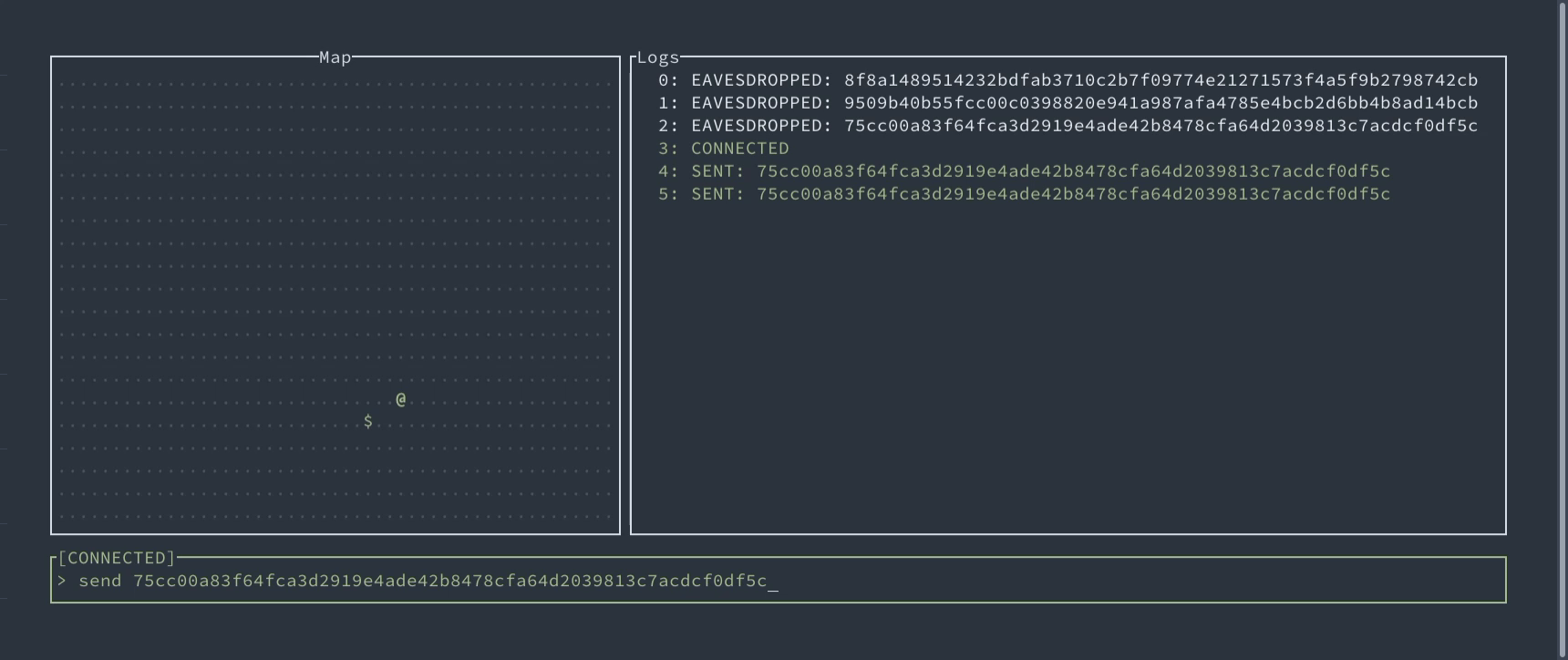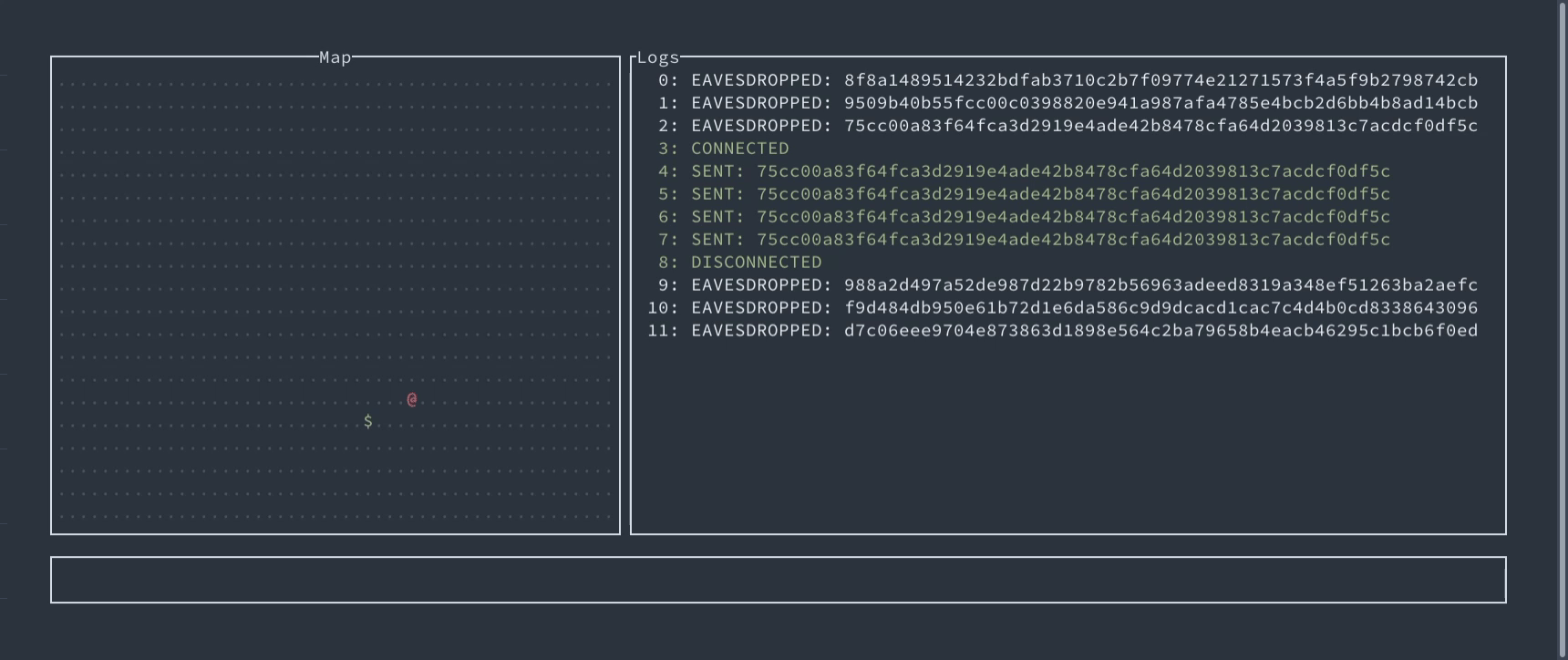
An interactive demo allows replaying movements of robotic device to control it.
How to prevent replay attacks? #
To prevent replay attacks, a tagging or synchronization mechanism must be used. The simplest way is to use a counter. Counter’s integrity must also be protected, or encrypted together with the original message.
Unfortunately, in the original audited system, no protection from replay attacks was implemented.
Encryption key is set to default if invalid is provided #
And finally—the dessert. 🎂
Quite often, users are the weakest points in the entire security system. They tend to make, and with enough time, always make errors. Therefore, in day-to-day life cryptographic engineers design systems that try to reduce the chances of human errors.
Let’s play a game called “Who wants to be a millionaire?" “Who wants to use cryptography?”. Imagine you have a system that requires entering a key in two places (so different parts of the system can communicate). It greets you with the following prompt:
E=
Your actions? Possible answers:
- enter a password
- enter a big number
- enter a hex-encoded key
- enter a base64-encoded key

But wait, this is not the end! You can also choose the length:
- 16 characters
- 32 characters
- 48 characters
- 64 characters
- 128 characters
- whatever big number of characters
In total, we’ve provided 24 possible combinations of answers. So, what would you choose?
The real answer is that the toy car radio firmware requires the end user to provide an encryption key for securing communication between the car and the controller.
The requirements for the key string is that it’s a hex-encoded string, which encodes 16, 24 or 32 bytes, so the string should contain 32, 48 or 64 characters, respectively. Is it documented somewhere? Yes! In the code!
So, there are:
- Only 3 possible valid combinations out of 24.
- If the user provides a hex string with more letters, it will be silently truncated, so another 2 options are somehow ok.
- If the user provides fewer characters—the system will tell that the length is too small and, best of all, will use the default hard-coded key! Isn’t that beautiful? :)
- If the user provides a string of required length but with non-hex characters, drum roll, each non-hex letter will silently be interpreted as a ‘0’ digit!
Could you imagine what percentage of weak or default keys was used in the wild? Neither do we.
If you want to try and play the game, we have a simulation for you. It prompts a key and shows the real key that would be used for these toy cars.
Interactive demo of bad key input API

An interactive demo to guess if encryption key you have entered will be used, or if the toy-car system will change it to an ‘ugly’ one.
How to avoid bad cryptographic design? #
Well… Designing cryptographic system should be accompanied by cryptographers.
Ensure that people-facing API is easy-to-use and hard-to-misuse. Validate input data and reject strings users input if they don’t match security criteria. Use tests. Audit your systems.
Consider using high-level cryptographic libraries that care about these things instead of you.
Real-world repercussions #
To sum it up, let’s add some real-life context: what could go wrong with toy cars, which operate software with cryptographic flaws we’ve found.
Let’s start with the tools we have.
Forging fake packets #
Adversaries can actively forge fake packets. In both cases (CTR and CBC), they can influence parts of the messages by bit flipping. Though in the CTR case, it’s much more fun because there is no way of getting noticed. The tag forging is also required, but it’s just as simple as the CRC-16 calculation.
Restoring encryption keys and secrets #
The adversaries are also able to restore keys and keystreams. They can run brute-forcing in parallel to search for weak or standard keys. In the CTR case, the adversaries can collect as many packets as they need to derive the full 48-byte keystream, which is used to encrypt every packet and is the same because of the static nonce. It’s feasible because they know the underlying protocol and possible values that are transmitted.
In the case of CBC mode, the adversaries can use magic padding oracles to decrypt the packets. It requires sending a couple of thousand messages via radio (on average, 128 messages for each byte, though in some cases it can be as low as 14 requests per byte), but if the decrypted text contains valuable information, like a key or a password, it’s worth it.
Causing DoS #
The static IV and nonce don’t hide the repetitions among the plaintexts. Together with the tininess of the packets, it allows the attackers to distinguish between protocol or data-related frames, even when they are encrypted. With no protection from replay attacks, they can reuse those packets because they don’t like environmental pollution and always try to give everything a second chance.
Breaking the system in various ways #
With such a powerful toolbox, the adversaries have an uncountable number of ways of intercepting and breaking the system. They are able to uncover communications contents and analyze traffic to predict the location of the toy cars. In some cases, they are able to craft their custom packets or reuse already seen ones to hijack the car or make it uncontrollable.
The capabilities of the combination of these attacks are limited only by the adversaries’ imagination (and antenna power).
Summary #
All the described problems were hidden in a rather short piece of the cryptographic code. And still we found numerous cryptographic failures and attack vectors. We doubt very much that all these opportunities for attacks were intentionally embedded in the design as features :).
The vulnerabilities come from misunderstanding cryptography primitives, their security requirements and guarantees, neglecting code hygiene, and secure system design principles.
As a result, almost every cryptographic aspect of the system is broken: encryption, integrity, side-channel attacks, and user interactions.
To sum it up, don’t roll your own crypto. Especially for moving robotic objects, please.
And if you are designing a system that requires a bit of cryptography (today this is almost every system), make sure to hire someone who knows what they’re doing or at least avoids so many damaging choices in one piece of code.


